1.5.2 There are many ways to skin a guanabana

But is this the only way to define an average? It makes sense because this is a procedure that could be implemented to any level of accuracy desired, and can be described by a real procedure: playing the game a zillion times. But there are other ways of defining the average that give the same results, but are easy to do calculations with. The drawback is that these methods don’t have the same air of reality, but if it makes calculation easier and it gives identical results, they’re probably worth considering.

Let’s concentrate on averaging the variable $x_5$. What is its probability distribution? It looks like this (fig 1.1).

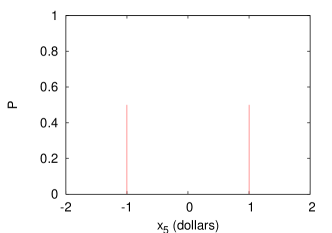
It’s $\frac{1}{2}$ if $x=\pm 1$, and $0$ otherwise. Let’s define the average of this distribution as

The sum is over all possible values that $x$ can take weighted by $P(x)$. In this case it’s $-1P(-1)+1P(1)=-1⁤\frac{1}{2}+1⁤\frac{1}{2}=0$.

You can see that in this example, these two definitions, the average over games, and the average over the probability distribution, are identical. We expect that this will be generally true. But averaging the second way is normally easier in practice, so we’ll stick with it. This definition, a sum weighted by $P(x)$ is something that we can do fairly easily if we know $P(x)$.

Another thing I should mention is that this kind of average is what I referred to above as an ”expectation value”. You’re averaging over an infinite number of games, so you’re getting a well defined result. Just a normal average, over say 10 games, would give you a different result every time you did it. So it makes more sense to deal with the case of a well converged result, the expectation value, rather than a result that fluctuates every time you do the experiment.